一次不定方程式137x+35y=1を満たす、整数x,yを求めよ。
このような不定方程式の問題の解き方を詳しく解説します。
また、記事の最後にはプログラミング言語Pythonを使って実装してみます。興味のある方は、ぜひ最後までご覧ください。
ユークリッドの互除法を使って2つの整数の最大公約数を求めるように、割り算を繰り返していく方法になります。
最大公約数を求める方法は、こちらの記事で紹介しています。→ユークリッドの互除法を使って最大公約数を求める方法
不定方程式ax + by = 1の整数解を求める方法
(1) 余りが1になるまで割り算を繰り返す
「大きい数÷小さい数」の計算を行い、商と余りを出します。
次に、「小さい数÷余り」の計算を行い、商と余りを出します。
これを、余りが1になるまで、どんどん繰り返していきます。
137x + 35y = 1の場合、次のようになります。
137÷35=3あまり32 → 32 = 137 – 35×3 …①
35÷32=1あまり3 → 3 = 35 – 32×1 …②
32÷3=10あまり2 → 2 = 32 – 3×10 …③
3÷2=1あまり1 → 1 = 3 – 2×1 …④
不定方程式ax+by=1を解く問題では、aとbは必ず「互いに素」の関係になります。そうでないと、整数aとbの組み合わせは存在しないことになってしまうからです。これについては別の機会に解説したいと思います。
そして、aとbが互いに素である場合は、割り算を繰り返すと、必ず余りが1になるときがやってくるのです。
(2) ax+by=1の形になるように、式を代入していく
さて、①~④の式を得ることができました。これらを組み合わせることで、
137x+35y=1という形の式を作ることができます。そうすれば、整数x,yの組み合わせを求めることができます。
①の右辺は、137と35で構成されています。ここがポイントです。
①の式を②に代入し、さらにそれを③に代入し…と繰り返していきます。
そして最終的に、④の式を137と35だけで構成させるというイメージです。
では、具体的にやっていきましょう。
①を②に代入します。そして、137と35で構成されるように式を整理して②’を作ります。
32 = 137 – 35×3 …①
3 = 35 – 32×1 …②
3 = 35 –(137 – 35×3)×1
= 137×(-1) + 35×4 …②’
②’を③に代入します。さらに、①も③に代入します。整理して③’を作ります。
3 = 137×(-1) + 35×4 …②’
32 = 137 – 35×3 …①
2 = 32 – 3×10 …③
2 = (137 – 35×3) – {137×(-1) + 35×4}×10
= 137×11 + 35×(-43) …③’
③’を④に代入します。さらに、②’を④に代入します。
2 = 137×11 + 35×(-43) …③’
3 = 137×(-1) + 35×4 …②’
1 = 3 – 2×1 …④
1 = {137×(-1) + 35×4} – {137×11 + 35×(-43)}×1
= 137×(-12) + 35×47
完成!
ということで、137x + 35y = 1の形になりました。
答えは、x=-12, y=47 となります。
今回のやり方を簡単に文章でまとめてみると、
・割り算を余りが1になるまで繰り返して、式を作る。
・最初の式を、以降の式に代入していって、最終的に1=ax+byの形にする。
という流れでした。
xとyの値が定まっていく過程
さて、ではここで、x,yがどのように求められていったのかを、おさらいを兼ねてみていきましょう。これは、Pythonのプログラムを書く際にも重要なアルゴリズムになりますので、よく見ていってください。
改めて、式を見てみましょう。
137x + 35y = 1
137÷35=3あまり32 → 32 = 137 – 35×3 …①
35÷32=1あまり3 → 3 = 35 – 32×1 …②
32÷3=10あまり2 → 2 = 32 – 3×10 …③
3÷2=1あまり1 → 1 = 3 – 2×1 …④
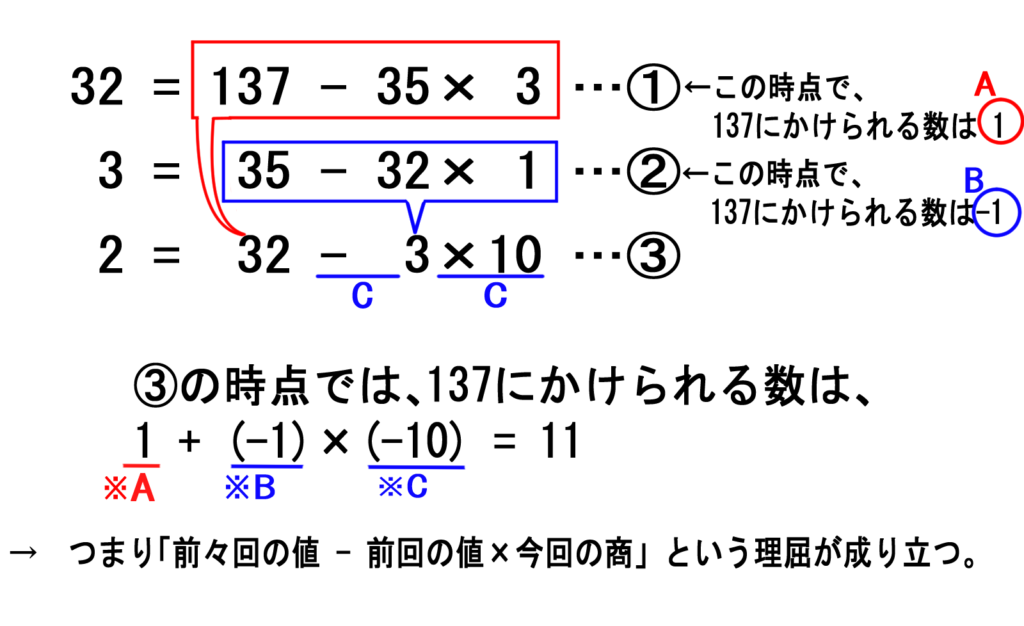
137にかけられる数xについてみていきます。(yもやり方は同じです)
STEP1
①の段階では、137×1なので、x=1ですね。
そして、①を②に代入します。
このとき、②の32には「-1」が掛けてありますので、
xの値は、1×(-1)= -1 ということになります。
STEP2
次に、③の式に代入します。
この時、③の3には「-10」が掛けてありますので、
xの値は、前回STEP1の「-1」に「-10」を掛けた値に更新されるわけです。
それに加えて、③の32の部分にも前々回の式①を代入することになります。
つまり、①の時のxの値「1」が追加されます。
結果として、今回STEP2では、xの値は(-1)×(-10)+1=11となります。
STEP3
次に、④の式に代入します。
STEP2と同様の流れになります。
・④の2に「-1」が掛けてあるので、前回STEP2のxの値「11」に「-1」を掛ける。
・④の3の部分には前々回の式を代入するので、前々回(STEP1)のxの値「-1」が追加される。
結果として、11×(-1) + (-1) = -12 となります。
というわけで、x=-12となるわけです。yの方も同様に考えることができます。
さて、割り算を余りが1になるまで繰り返した後、xやyを求めるにあたって、次のような理屈が成り立つことが分かります。
・前回までで求めたx,yに、商×(-1)を掛けた値。
・前々回までで求めたx,y。
・上記2つを足したものが、今回のx,y
→ 今回のx,y = 前々回のx,y – 前回のx,y ×今回の商
また、ax+by=1で、a>bのとき、最初の段階では、xの値は必ず1になります。
一方で、yの値は(a÷bの商)×(-1)になります。
Pythonで不定方程式を求めてみる
理屈が分かれば、Pythonで実装することができます。まずは、サンプルコードを見てみましょう。
## ax + by = 1 の整数解x,yを求める。
def func(a,b):
# a>bの関係にしておく
a,b = (b,a) if a<b else (a,b)
pre_x, now_x = 1,0 # xの値は、最初は1
pre_y, now_y = 0,1 # yの値は、最初は商x(-1)
while True:
# 商
q = a//b
# 「前々回の係数合計 - 前回の係数合計に商をかけた値」が今回の係数合計になる。
pre_x, now_x = now_x, pre_x - now_x * q
pre_y, now_y = now_y, pre_y - now_y * q
if a%b == 1: # 余りが1でループを抜け終了
break
elif a%b == 0: # 余りが1になる前に0になってしまった場合
print('aとbは互いに素ではないので、不定方程式ax+by=1を満たす整数x,yは存在しません。')
return None, None
# 割られる数, 割る数 = 割る数, 余り
a, b = b, a%b
return now_x, now_y
# 137x + 35y = 1
a = 137
b = 35
x,y = func(a,b)
if x:
print(f'{a}x({x})+{b}x({y})={a*x + b*y}')# 出力結果:
137x(-12)+35x(47)=1プログラムでは、ax+by=1のa,bを引数として入れると、整数解x,yを戻り値とするfunc関数を書いています。では、詳細を見ていきましょう。
5行目では、与えられた2つの引数がa>bという関係になるように直しています。
7,8行目では、xとyの値を最初に変数で定義しています。10行目以降のwhile文でその値が変化していきます。思い出していただきたいのですが、xとyを求めるアルゴリズムは以下のようなものでした。
・前回までで求めたx,yに、商×(-1)を掛けた値。
・前々回までで求めたx,y。
・上記2つを足したものが、今回のx,y
→ 今回のx,y = 前々回のx,y – 前回のx,y ×今回の商
つまり、「前々回の値」と「前回の値」の2つを記憶しておく必要があります。
そのため、xとyでそれぞれ2つずつの変数を用意しているのです。
最初の段階ではxの値は、1になります。yの値は、割り算をしたときの商x(-1)になります。
そのことを踏まえると、あらかじめ、
pre_x =1, now_x = 0
pre_y = 0, now_y = 1
としておくと、ちょうど計算が合います。
12行目では、a÷bの商を変数qに代入しています。
15行目ではxの値、16行目ではyの値を更新しています。
ここで重要になってくるのが、このアルゴリズムです。
・前回までで求めたx,yに、商×(-1)を掛けた値。
・前々回までで求めたx,y。
・上記2つを足したものが、今回のx,y
→ 今回のx,y = 前々回のx,y – 前回のx,y ×今回の商
今回のxの値(now_x)には、前々回のxの値(pre_x) – 前回のxの値(now_x)×商(q)が新たに代入されることになるわけです。yも全く同様です。
18行目では、余りが1になったらwhile文を脱出するコードを書いています。
20行目では、余りが0になった場合に、イレギュラー発生のために関数内処理を終わらせる旨を書いています。
今回のような不定方程式では、aとbは互いに素でなければなりません。
割り算を繰り返しているうちに、余りが1になる前に0になってしまったら、それは互いに素ではないということになります。2以上の整数で割り切れてしまうというわけですから。よって、整数解x,yを持つ不定方程式自体が成り立たないのです。
24行目では、割る数と割られる数を更新するコードを書いています。
a÷b の割り算を行い商と余りを計算したとき、次のループではbが割られる数、余りが割る数になるわけです。
最後に、27行目で最終更新したxとyの値を戻り値としてreturnしています。



コメント