こんにちは、かぐーです!
今回のテーマは、高校数学で学ぶ「ユークリッドの互除法」です。
ユークリッドの互除法を使って最大公約数を求めるやり方を、図を使ってわかりやすく解説していきます。
また、最後にはプログラミング言語pythonを使って、ユークリッドの互除法を再現するプログラムを作ってみます。
学生の方も、プログラミングを勉強している方も、どちらの方にも有益な内容となっておりますので、ぜひ最後までお付き合いくださいませ。
ユークリッドの互除法とは?
2つの自然数a,bに対して、
a=bq+rであるならば、aとbの最大公約数は、bとrの最大公約数と同じである。
a=bq+rの部分を言い換えると、「aをbで割った商がq、余りがr」ということになります。
図であらわしてみましょう。
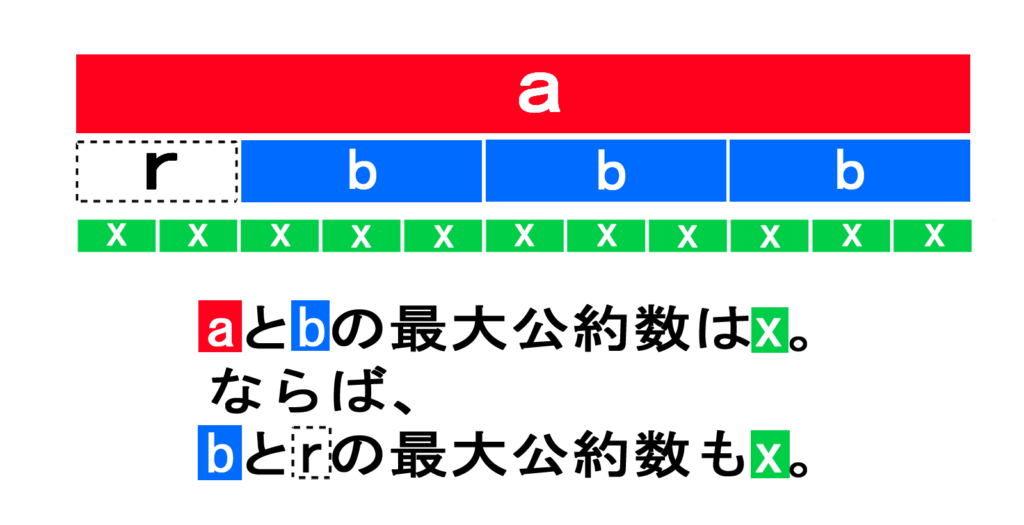
aはxで割り切れて、bもxで割り切れるとします。であれば、余りrも、xで割り切れるはずです。
もし、rがxで綺麗に割り切れないならば、aもxで割り切れなくなってしまうはずなのですから。
例えば、 a=22,b=6 のとき。
22=6×3 + 4 になります。22と6の最大公約数は「2」になり、6と4の最大公約数も「2」になります。
数学的な証明は割愛しますが、状況をイメージしやすくなったのではないでしょうか。
2つの整数の最大公約数を求める
ユークリッドの互除法を使うと、2つの整数の最大公約数を計算で求めることができます。
「a = bq + r」では、aをbで割ったときの商がq, 余りがrという関係になります。
このとき、割った数bと余りrの最大公約数が、aとbの最大公約数と同じであることを利用した方法になります。
その方法は以下の通りです。
- 大きい数を小さい数で割って、商と余りを求める。
- 小さい数を余りで割って、その商と余りを求める。
- 同様に「割った数」を「余り」で割る作業を繰り返す。
- 余りが0になったら、その時に「割った数」が最大公約数になる。
bをrで割って0になるということは、その時「割った数」がbとrの最大公約数ということになり、結局aとbの最大公約数でもあるという寸法です。
具体的に、24と9でやってみましょう。
- 24÷9=2あまり6 (24と9の最大公約数は、9と6の最大公約数)
- 9÷6=1あまり3 (9と6の最大公約数は、6と3の最大公約数)
- 6÷3=2あまり0 (6と3の最大公約数は、3)
「3」は6と3の最大公約数であり、つまり、24と9の最大公約数。
さて、一体何が起きているのか、ここからは図を使ってみていきましょう。
① 24と9の最大公約数、第一候補は「9」
大きい数と小さい数があれば、小さい数が最大公約数の第一候補になります。(厳密には絶対数の小さい数字)24と9の場合は「9」です。
24÷9=2…6
6余ってしまうので、「9」は最大公約数ではないようです。

例えば、24と8だったら、24÷8=3 で割り切れるから、
「8」が最大公約数になるんだね。
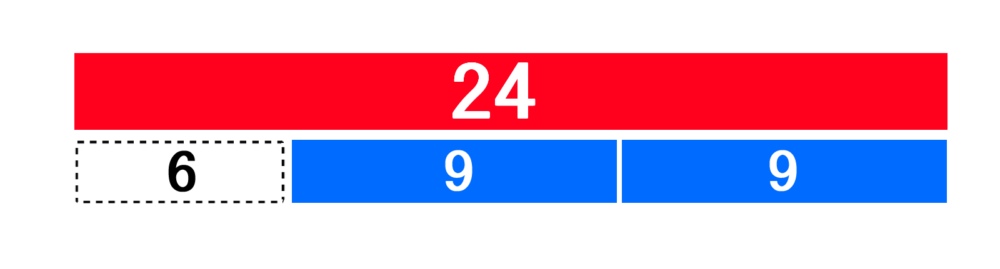
② 24と9の最大公約数、第二候補は「6」
先ほど、6が余ってしまったので、次に24と9の最大公約数になる候補は、この「6」になります。
もし、24と9がどちらも6で割り切れるなら、次の図のような状態になります。

24は「6」だけで構成することができるし、9も「6」だけで構成できる。これが公約数というものです。
しかし、9÷6=1…3
と3余ってしまうので、これも違います。
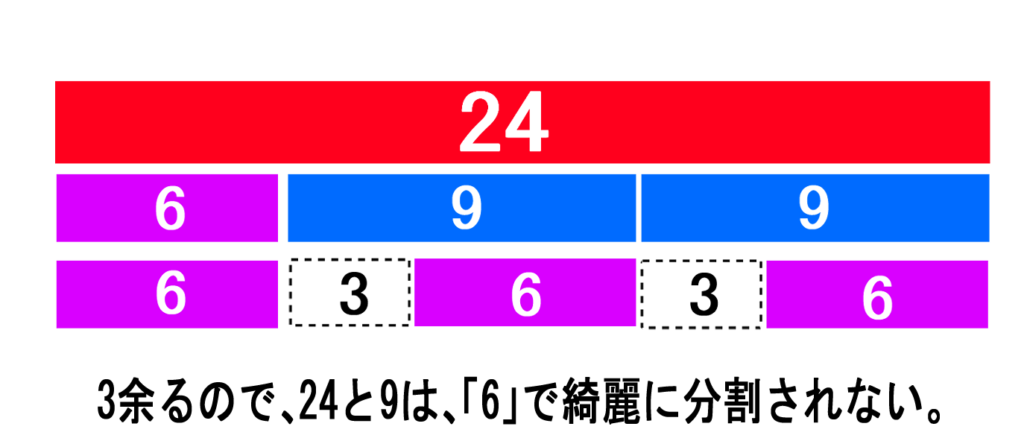
余ってしまうということは、6は9の約数ではありません。当然、24と9の最大公約数ではないということになります。
③ 24と9の最大公約数、第三候補は「3」
今度は、余った3が、24と9の最大公約数の次の候補となります。
6÷3=2
今度は余りが出ません! つまり、次の図のようになります。
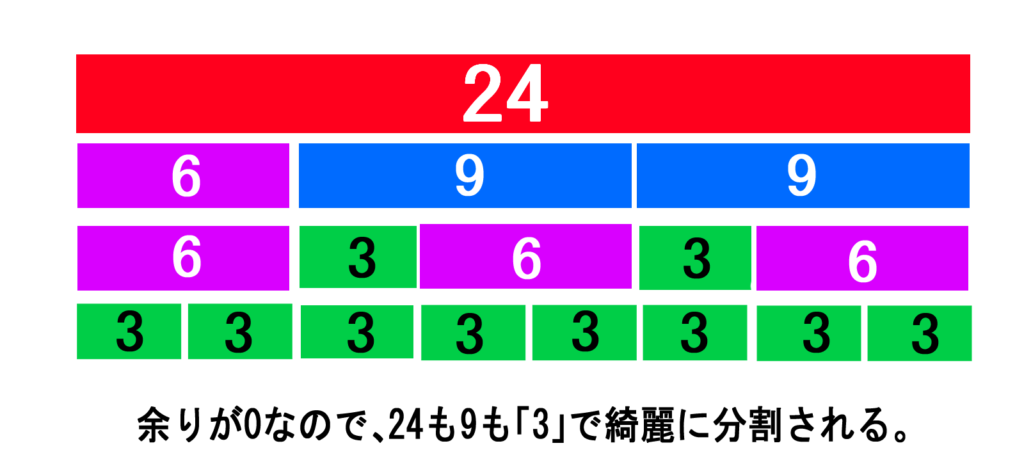
余りが出ないということは、ここで初めて、全て同じ値(3)で分割できるということになります。
図を見ると、24も9も「3」で分割されているのがわかります。
この段階で初めて、24と9の公約数が登場しました。つまり、24と9の最大公約数は3であるということになるのです。
最大公約数を求めるプログラムをPythonで実装してみる
ユークリッドの互除法を使って、最大公約数を求める方法をPythonで表現してみました。
やり方のポイントをおさらいしましょう。
- 大きい数を小さい数で割って、商と余りを求める。
- 小さい数を余りで割って、その商と余りを求める。
- 同様に「割った数」を「余り」で割る作業を繰り返す。
- 余りが0になったら、その時に「割った数」が最大公約数になる。
割る数と割られる数を変化させながら、割り切れるまで作業を繰り返すので、while文でループする必要が出てきますね。また、割り切れたらループを抜け出すコードも書かないといけません。
一例ですが、次のようなコードになります。
a = 24
b = 9
while True:
# 割り切れたら終了。割った数bが最大公約数
if a%b == 0:
break
# 割り切れなかったら、「割る数」「割られる数」を変更。
a, b = b, a%b
print('最大公約数は', b, 'です。')

コメント